
Water has a much easier time moving around, and the water wants to bulge in the direction of the moon. When the moon's gravity pulls on the water in the oceans, however, someone's bound to notice. The moon's gravity even pulls on the land, but not enough for anyone to tell (unless they use special, really precise instruments).

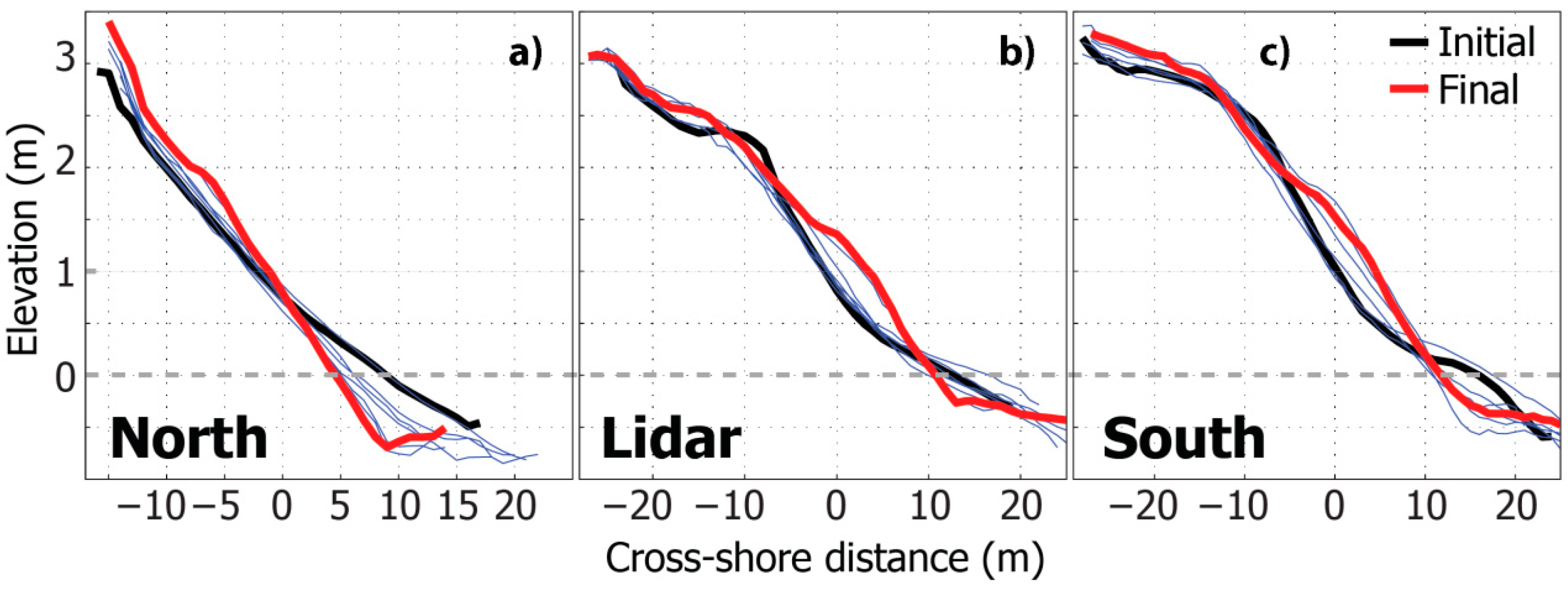
Even though the moon only has about 1/100th the mass of Earth, since it's so close to us, it has enough gravity to move things around. Tides are really all about gravity, and when we're talking about the daily tides, it's the moon's gravity that's causing them.Īs Earth rotates, the moon's gravity pulls on different parts of our planet. As regions of Earth pass through the bulges, they can experiences a high tide. This animation shows the tidal force in a view of Earth from the North Pole. This cycle of two high tides and two low tides occurs most days on most of the coastlines of the world. When you're not in one of the bulges, you experience a low tide. When you're in one of the bulges, you experience a high tide. Photo by Samuel Wantman.Īs the Earth rotates, your region of Earth passes through both of these bulges each day. Image credit: Wikimedia Commons, Tttrung. High tide (left) and low tide (right) in the Bay of Fundy in Canada. The tidal force causes Earth-and its water-to bulge out on the side closest to the moon and the side farthest from the moon. The moon's gravitational pull generates something called the tidal force. Nodal modulation is also found for the S 2 constituent (in theory, the S 2 has no nodal modulation), which is 0.8% averaged at 164 tide gauges where the S 2 is not too weak.High tides and low tides are caused by the moon. On the global scale, the nodal modulations of the M 2, K 1 and O 1 constituents agree with the theoretical predictions, except a cold spot region with reduced nodal modulation in the Gulf of Maine and a hot spot region with enhanced nodal modulation in the South China Sea for the M 2. The nodal modulations of predominant constituents are also explored in this study. Compared with the new method, some adaptations to traditional HA aiming to capture variations in amplitudes and phase lags of constituents have some limitations, because they either neglect some satellites of the major constitutes or introduce spurious fluctuations resulting from an unreasonably large number of independent points. Because the frequency of the H 1 (H 2) constituent is equal to that of the M 2 minus (plus) the frequency of annual cycles, the superposition of the M 2, H 1 and H 2 constituents with constant amplitudes is equivalent to the M 2 constituent with seasonally varying amplitudes.

The seasonal variations of the M 2 constituent reported in previous studies are caused by its satellites, the H 1 and H 2 constituents, which are not resolved in these studies due to the short time window (one month or three months) used in HA. However, based on the newly proposed method of modified two-step harmonic analysis (HA) and its application at 240 global tide gauges, we find that the M 2 constituent as well as the S 2 and K 1 do not have significant seasonal variations at these tide gauges. Previous studies have reported that the M 2 constituent exhibits seasonal variations (annual cycles) in some regions.
Tides are one of the basic types of ocean water motions.


 0 kommentar(er)
0 kommentar(er)
